前言
发现还是得比较细致地了解一下常见的加密算法(想特别深入地了解,感觉目前水平做不到,需要特别强的数学功底。),这样比赛的时候或者实战的时候,能更加快地去定位到它所使用的加密算法。 你会说,为什么不用findcrypt这样的插件,感觉还是不能依赖,而且很多魔改过的加密其实这个插件也都识别不出来。 所以争取在国赛前,把目前碰到的一些加密算法都尽可能更深入地了解一下。希望今年的国赛,能为团队出点力,争取拿个奖吧!
单向散列算法
MD5
加密步骤
1.对明文进行Hex编码
比如
Fup1p1 -> 46 75 70 31 70 31
2.填充(Padding)
因为md5是一组一组加密的,一组的长度是512bit,所以如果你输入的长度不足448bit,那么就需要填充,也就是padding。
怎么padding呢?
先填充一个1,然后后面跟上对应个数的0
搜嘎,也就是 1000 0000 0000 0000 ..... ->hex 80 00 ...
但是为什么是填充到448bit,而不是填充至512bit呢?
因为剩余的64bit需要表示消息长度!那么如果消息长度大于2^64呢?那就取最低64bit!而且,注意是小端序(MD5算法使用的是小端序字节序)!!!这同时也是为什么md5加密不限制长度的原因。
那么如果我的数据长度大于448bit,但是小于512bit,又怎么添加64bit的消息长度呢?
这时候,就需要填充的时候,填充长度至模512能刚好被448整除为止。
3.将明文进行分组,分成16块(M1~M16)
512 bit/16 = 32bit
4.初始化MD5常量
A=0x67452301 B=0xefcdab89 C=0x98badcfe D=0x10325476
5.MD5Transform(核心)
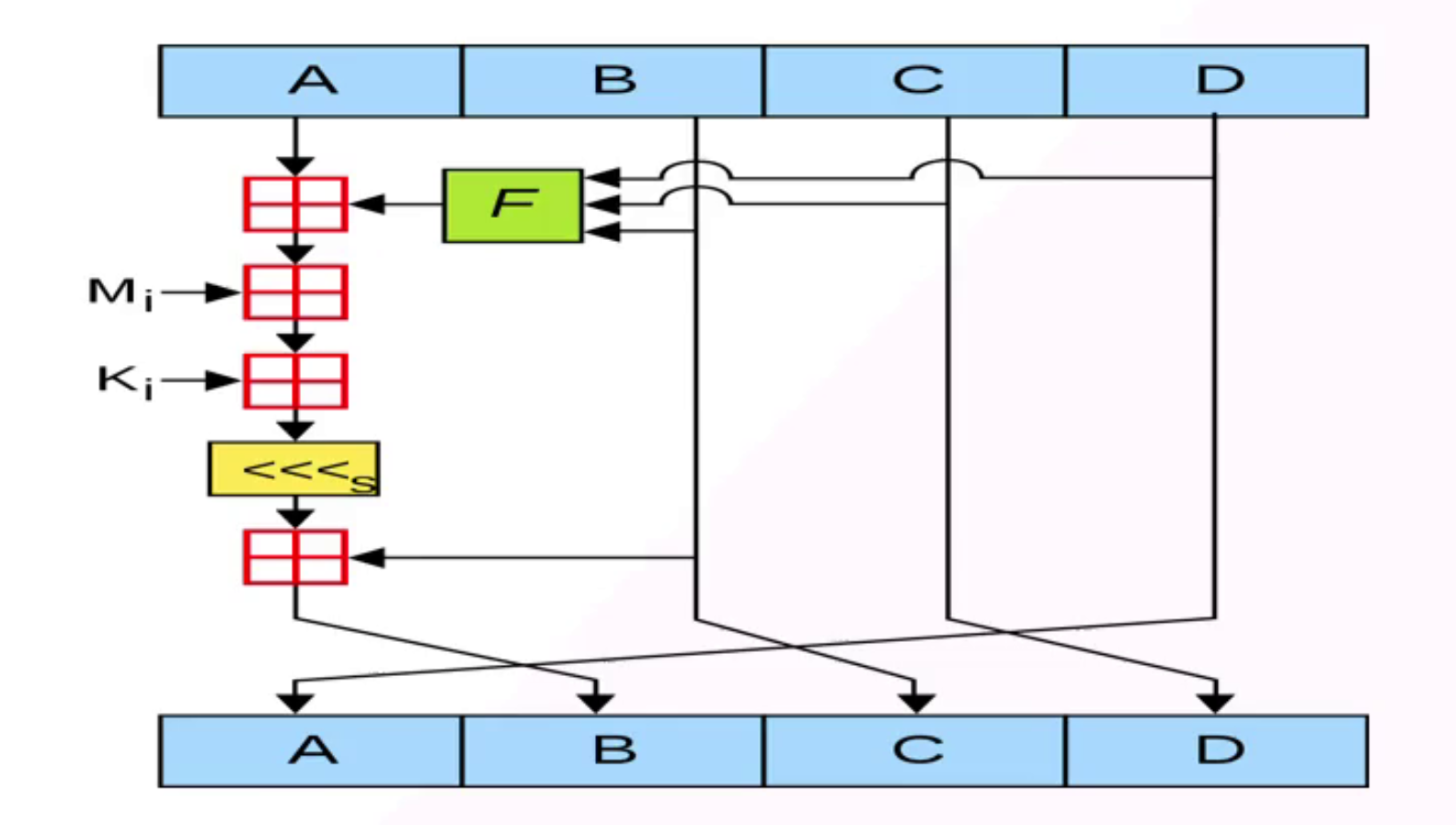 MD5的核心就是重复这个运算64次(也可以理解为4轮运算,重复16次)。这个运算也很明显,每一轮计算一个常量的值,然后其他三个常量的值只是换位。
MD5的核心就是重复这个运算64次(也可以理解为4轮运算,重复16次)。这个运算也很明显,每一轮计算一个常量的值,然后其他三个常量的值只是换位。
• 图中的田 代表相加
• 图中的F函数是由四个函数组合而成的
• K表在代码中体现为常量(为了效率),但是其实有公式去计算的 2^32*(int)abs(sin(i)), i从1到64。
• <<<s 代表的是循环左移!s是定值,或者有一个表。这个值一般不会改。(有安全性问题的SHA0,通过循环左移1位,解决了这个问题,也就是后面我们经常使用到的SHA1)
• 最后四个初始化常量不断变化后得到的值,拼接后就是最终的摘要结果。
FF(a,b,c,d,Mj,s,ti) a=b+(a+F(b,c,d)+Mj+ti)<<s
GG(a,b,c,d,Mj,s,ti) a=b+(a+G(b,c,d)+Mj+ti)<< s
HH(a,b,c,d,Mj,s,ti) a=b+(a+H(b,c,d)+Mj+ti)<< s
II(a,b,c,d,Mj,s,ti) a=b+(a+I(b,c,d)+Mj+ti)<< s
找一份C实现的源码来分析(当然,有很多实现方式,下面源码只是一种)
//MD5.h
#ifndef HOOKDEMO_MD5_H
#define HOOKDEMO_MD5_H
typedef struct {
unsigned int count[2];//分成两个数组来存放长度的bit。
unsigned int state[4];//存放计算后四个常量
unsigned char buffer[64];//缓冲区
} MD5_CTX;
#define F(x,y,z) ((x & y) | (~x & z))
#define G(x,y,z) ((x & z) | (y & ~z))
#define H(x,y,z) (x^y^z)
#define I(x,y,z) (y ^ (x | ~z))
#define ROTATE_LEFT(x,n) ((x << n) | (x >> (32-n)))
#define FF(a,b,c,d,x,s,ac) \
{ \
a += F(b,c,d) + x + ac; \
a = ROTATE_LEFT(a,s); \
a += b; \
}
#define GG(a,b,c,d,x,s,ac) \
{ \
a += G(b,c,d) + x + ac; \
a = ROTATE_LEFT(a,s); \
a += b; \
}
#define HH(a,b,c,d,x,s,ac) \
{ \
a += H(b,c,d) + x + ac; \
a = ROTATE_LEFT(a,s); \
a += b; \
}
#define II(a,b,c,d,x,s,ac) \
{ \
a += I(b,c,d) + x + ac; \
a = ROTATE_LEFT(a,s); \
a += b; \
}
void MD5Init(MD5_CTX* context);
void MD5Update(MD5_CTX* context, unsigned char* input, unsigned int inputlen);
void MD5Final(MD5_CTX* context, unsigned char digest[16]);
void MD5Transform(unsigned int state[4], unsigned char block[64]);
void MD5Encode(unsigned char* output, unsigned int* input, unsigned int len);
void MD5Decode(unsigned int* output, unsigned char* input, unsigned int len);
#endif //HOOKDEMO_MD5_H
#include <iostream>
#include <memory.h>
#include <string.h>
#include "MD5.h"
using namespace std;
unsigned char PADDING[] = {0x80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
void MD5Init(MD5_CTX *context) {
context->count[0] = 0;
context->count[1] = 0;
context->state[0] = 0x67452301;
context->state[1] = 0xEFCDAB89;
context->state[2] = 0x98BADCFE;
context->state[3] = 0x10325476;
}
void MD5Update(MD5_CTX *context, unsigned char *input, unsigned int inputlen) {
unsigned int i = 0, index = 0, partlen = 0;
index = (context->count[0] >> 3)
partlen = 64 - index;
context->count[0] += inputlen << 3;& 0x3F;//字节转换成bit
if (context->count[0] < (inputlen << 3))如果溢出
context->count[1]++;//为什么需要+1,因为分成了两个数组来存放高位32和低位32,由于无符号32位只能存2^32-1,所以在进位的时候还得补上一个1!
context->count[1] += inputlen >> 29; //count[1]存放高位32数据。
if (inputlen >= partlen) { //如果大于512bit,就直接transform了
memcpy(&context->buffer[index], input, partlen);
MD5Transform(context->state, context->buffer);
for (i = partlen; i + 64 <= inputlen; i += 64)
MD5Transform(context->state, &input[i]);
index = 0;
} else {
i = 0;
}
memcpy(&context->buffer[index], &input[i], inputlen - i);
}
void MD5Final(MD5_CTX *context, unsigned char digest[16]) {
unsigned int index = 0, padlen = 0;
unsigned char bits[8];
index = (context->count[0] >> 3) & 0x3F;
padlen = (index < 56) ? (56 - index) : (120 - index);
MD5Encode(bits, context->count, 8); //对消息程度进行了端序转换
MD5Update(context, PADDING, padlen);// 填充padding
MD5Update(context, bits, 8); // 填充最后的64bit(消息长度)
printf("%.8x\n", context->state[0]);
printf("%.8x\n", context->state[1]);
printf("%.8x\n", context->state[2]);
printf("%.8x\n", context->state[3]);
MD5Encode(digest, context->state, 16); //端序转换
}
void MD5Encode(unsigned char *output, unsigned int *input, unsigned int len) {
unsigned int i = 0, j = 0;
while (j < len) {
output[j] = input[i] & 0xFF;
output[j + 1] = (input[i] >> 8) & 0xFF;
output[j + 2] = (input[i] >> 16) & 0xFF;
output[j + 3] = (input[i] >> 24) & 0xFF;
i++;
j += 4;
}
}
void MD5Decode(unsigned int *output, unsigned char *input, unsigned int len) {
unsigned int i = 0, j = 0;
while (j < len) {
output[i] = (input[j]) |
(input[j + 1] << 8) |
(input[j + 2] << 16) |
(input[j + 3] << 24);
i++;
j += 4;
}
}
void MD5Transform(unsigned int state[4], unsigned char block[64]) { //这么写可能会很冗余,有些写法是直接switch case,比较美观,因为这64轮加密实际上就是4轮加密,每轮运算16次。
unsigned int a = state[0];
unsigned int b = state[1];
unsigned int c = state[2];
unsigned int d = state[3];
unsigned int x[64];
MD5Decode(x, block, 64);
FF(a, b, c, d, x[0], 7, 0xd76aa478); /* 1 */
FF(d, a, b, c, x[1], 12, 0xe8c7b756); /* 2 */
FF(c, d, a, b, x[2], 17, 0x242070db); /* 3 */
FF(b, c, d, a, x[3], 22, 0xc1bdceee); /* 4 */
FF(a, b, c, d, x[4], 7, 0xf57c0faf); /* 5 */
FF(d, a, b, c, x[5], 12, 0x4787c62a); /* 6 */
FF(c, d, a, b, x[6], 17, 0xa8304613); /* 7 */
FF(b, c, d, a, x[7], 22, 0xfd469501); /* 8 */
FF(a, b, c, d, x[8], 7, 0x698098d8); /* 9 */
FF(d, a, b, c, x[9], 12, 0x8b44f7af); /* 10 */
FF(c, d, a, b, x[10], 17, 0xffff5bb1); /* 11 */
FF(b, c, d, a, x[11], 22, 0x895cd7be); /* 12 */
FF(a, b, c, d, x[12], 7, 0x6b901122); /* 13 */
FF(d, a, b, c, x[13], 12, 0xfd987193); /* 14 */
FF(c, d, a, b, x[14], 17, 0xa679438e); /* 15 */
FF(b, c, d, a, x[15], 22, 0x49b40821); /* 16 */
/* Round 2 */
GG(a, b, c, d, x[1], 5, 0xf61e2562); /* 17 */
GG(d, a, b, c, x[6], 9, 0xc040b340); /* 18 */
GG(c, d, a, b, x[11], 14, 0x265e5a51); /* 19 */
GG(b, c, d, a, x[0], 20, 0xe9b6c7aa); /* 20 */
GG(a, b, c, d, x[5], 5, 0xd62f105d); /* 21 */
GG(d, a, b, c, x[10], 9, 0x2441453); /* 22 */
GG(c, d, a, b, x[15], 14, 0xd8a1e681); /* 23 */
GG(b, c, d, a, x[4], 20, 0xe7d3fbc8); /* 24 */
GG(a, b, c, d, x[9], 5, 0x21e1cde6); /* 25 */
GG(d, a, b, c, x[14], 9, 0xc33707d6); /* 26 */
GG(c, d, a, b, x[3], 14, 0xf4d50d87); /* 27 */
GG(b, c, d, a, x[8], 20, 0x455a14ed); /* 28 */
GG(a, b, c, d, x[13], 5, 0xa9e3e905); /* 29 */
GG(d, a, b, c, x[2], 9, 0xfcefa3f8); /* 30 */
GG(c, d, a, b, x[7], 14, 0x676f02d9); /* 31 */
GG(b, c, d, a, x[12], 20, 0x8d2a4c8a); /* 32 */
/* Round 3 */
HH(a, b, c, d, x[5], 4, 0xfffa3942); /* 33 */
HH(d, a, b, c, x[8], 11, 0x8771f681); /* 34 */
HH(c, d, a, b, x[11], 16, 0x6d9d6122); /* 35 */
HH(b, c, d, a, x[14], 23, 0xfde5380c); /* 36 */
HH(a, b, c, d, x[1], 4, 0xa4beea44); /* 37 */
HH(d, a, b, c, x[4], 11, 0x4bdecfa9); /* 38 */
HH(c, d, a, b, x[7], 16, 0xf6bb4b60); /* 39 */
HH(b, c, d, a, x[10], 23, 0xbebfbc70); /* 40 */
HH(a, b, c, d, x[13], 4, 0x289b7ec6); /* 41 */
HH(d, a, b, c, x[0], 11, 0xeaa127fa); /* 42 */
HH(c, d, a, b, x[3], 16, 0xd4ef3085); /* 43 */
HH(b, c, d, a, x[6], 23, 0x4881d05); /* 44 */
HH(a, b, c, d, x[9], 4, 0xd9d4d039); /* 45 */
HH(d, a, b, c, x[12], 11, 0xe6db99e5); /* 46 */
HH(c, d, a, b, x[15], 16, 0x1fa27cf8); /* 47 */
HH(b, c, d, a, x[2], 23, 0xc4ac5665); /* 48 */
/* Round 4 */
II(a, b, c, d, x[0], 6, 0xf4292244); /* 49 */
II(d, a, b, c, x[7], 10, 0x432aff97); /* 50 */
II(c, d, a, b, x[14], 15, 0xab9423a7); /* 51 */
II(b, c, d, a, x[5], 21, 0xfc93a039); /* 52 */
II(a, b, c, d, x[12], 6, 0x655b59c3); /* 53 */
II(d, a, b, c, x[3], 10, 0x8f0ccc92); /* 54 */
II(c, d, a, b, x[10], 15, 0xffeff47d); /* 55 */
II(b, c, d, a, x[1], 21, 0x85845dd1); /* 56 */
II(a, b, c, d, x[8], 6, 0x6fa87e4f); /* 57 */
II(d, a, b, c, x[15], 10, 0xfe2ce6e0); /* 58 */
II(c, d, a, b, x[6], 15, 0xa3014314); /* 59 */
II(b, c, d, a, x[13], 21, 0x4e0811a1); /* 60 */
II(a, b, c, d, x[4], 6, 0xf7537e82); /* 61 */
II(d, a, b, c, x[11], 10, 0xbd3af235); /* 62 */
II(c, d, a, b, x[2], 15, 0x2ad7d2bb); /* 63 */
II(b, c, d, a, x[9], 21, 0xeb86d391); /* 64 */
state[0] += a;
state[1] += b;
state[2] += c;
state[3] += d;
}
int main(){
// void MD5Init(MD5_CTX *context);
MD5_CTX context;
MD5Init(&context);
// void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen);
unsigned char* plainText = (unsigned char *) "Fup1p1";
MD5Update(&context, plainText, strlen(reinterpret_cast<const char *>(plainText)));
// void MD5Final(MD5_CTX *context,unsigned char digest[16]);
unsigned char result[16];
MD5Final(&context, result);//对最后一段进行填充、计算。
char temp[2] = {0};
char finalResult[33] = {0};
for(int i = 0; i < 16; i++){
int index = i;
sprintf(temp, "%.2x", result[index]);
strcat(finalResult, temp);
}
cout << finalResult << endl;
return 0;
}
SHA1
和MD5一样,都是由MD4改进过来的,很多加密步骤和MD5非常类似。
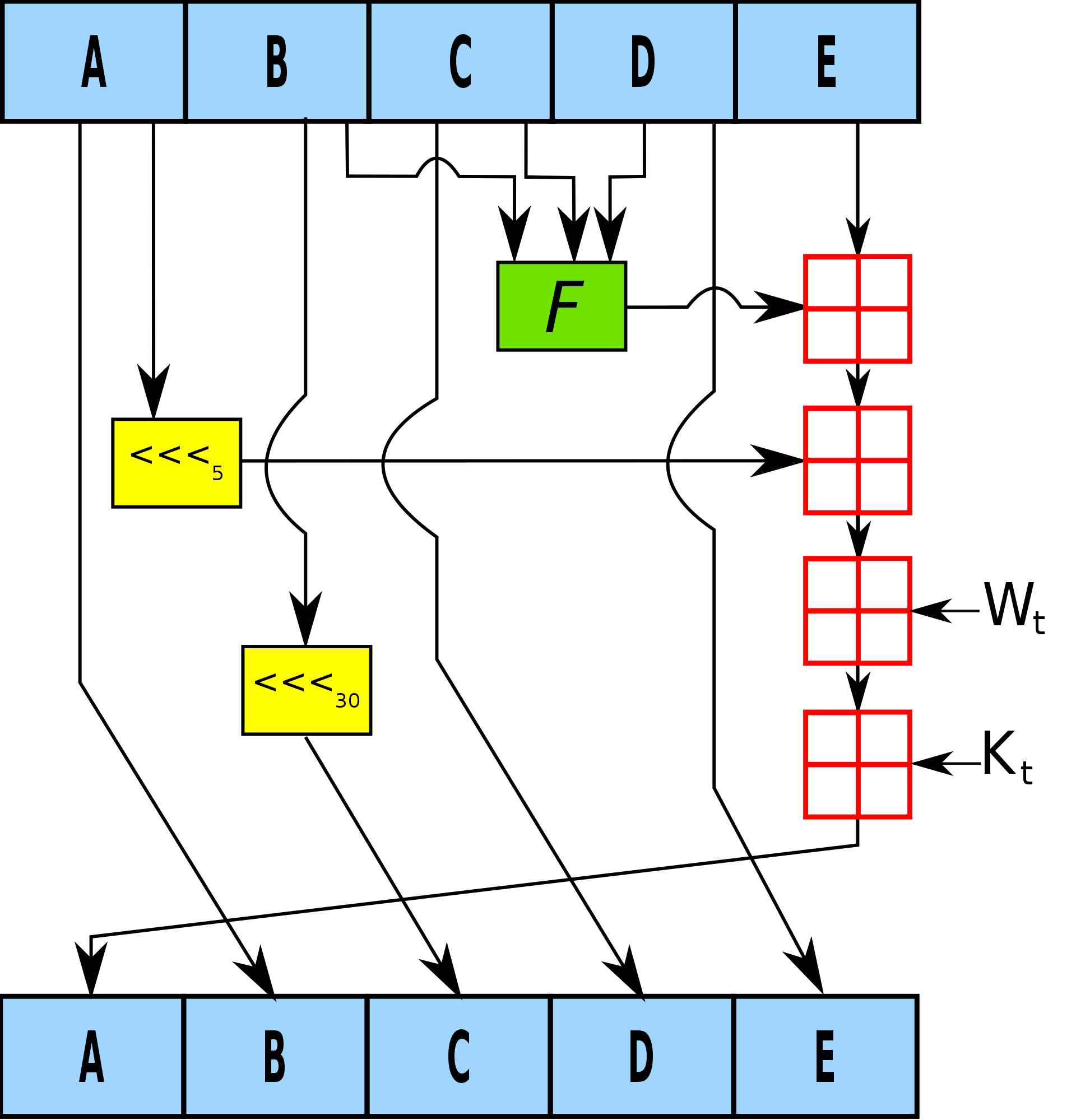
字节序
和MD5的小端序不同,SHA1是大端序!并且加密中也用到的也都是大端序!
初始化常量是5个
前四个常量和MD5一样,多了一个常量。 0x67452301 0xEFCDAB89 0x98BADCFE 0x10325476 0xC3D2E1F0
分组
分组长度也是512bit,明文也要分段,但是要分成80段,相比较于MD5的16段,多出的64段是扩展出来的,并且遵循大端序的字节。
但是在分组计算的时候,又和MD5不太一样。
MD5的M盒变换
void MD5Decode(unsigned int* output, unsigned char* input, unsigned int len) {
unsigned int i = 0, j = 0;
while (j < len) {
output[i] = (input[j]) |
(input[j + 1] << 8) |
(input[j + 2] << 16) |
(input[j + 3] << 24);
i++;
j += 4;
}
}
SHA1的W盒变换
for (t = 0; t < 16; t++) {
W[t] = context->Message_Block[t * 4] << 24; //很明显,和上面的MD5的区别就只是端序问题了!
W[t] |= context->Message_Block[t * 4 + 1] << 16;
W[t] |= context->Message_Block[t * 4 + 2] << 8;
W[t] |= context->Message_Block[t * 4 + 3];
}
然后多了64轮
for (t = 16; t < 80; t++) {
W[t] = SHA1CircularShift(1, W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16]);
//W[t] = W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16]; SHA0是这样子的,就少了一个循环左移,却存在安全问题。
}
分组计算(核心)
SHA1 分为4轮,每轮20次计算,总共也就是80组,其中的压缩函数也与MD5不同,sha1每轮加上的是一个定值,后面代码中体现是一个K表(4个常量)。而MD5加上的是2^32 * abs(sin(i))。
源码分析(偷了一份代码来分析)
//sha1.h
#ifndef _SHA1_H_
#define _SHA1_H_
#include <stdint.h>
#ifndef _SHA_enum_
#define _SHA_enum_
enum {
shaSuccess = 0,
shaNull, /* Null pointer parameter */
shaInputTooLong, /* input data too long */
shaStateError /* called Input after Result */
};
#endif
#define SHA1HashSize 20
typedef struct SHA1Context {
uint32_t Intermediate_Hash[SHA1HashSize / 4]; /* Message Digest */
uint32_t Length_Low; /* Message length in bits */
uint32_t Length_High; /* Message length in bits */
/* Index into message block array */
int_least16_t Message_Block_Index;
uint8_t Message_Block[64]; /* 512-bit message blocks */
int Computed; /* Is the digest computed? */
int Corrupted; /* Is the message digest corrupted? */
} SHA1Context;
int SHA1Reset(SHA1Context *);
int SHA1Input(SHA1Context *, const uint8_t *, unsigned int);
int SHA1Result(SHA1Context *, uint8_t Message_Digest[SHA1HashSize]);
#endif
#include <stdio.h>
#include "sha1.h"
#ifdef __cplusplus
extern "C"
{
#endif
#define SHA1CircularShift(bits, word) \
(((word) << (bits)) | ((word) >> (32-(bits))))
void SHA1PadMessage(SHA1Context *);
void SHA1ProcessMessageBlock(SHA1Context *);
int SHA1Reset(SHA1Context *context)//初始化状态
{
if (!context) {
return shaNull;
}
context->Length_Low = 0;
context->Length_High = 0;
context->Message_Block_Index = 0;
context->Intermediate_Hash[0] = 0x67452301;//取得的HASH结果(中间数据)
context->Intermediate_Hash[1] = 0xEFCDAB89;
context->Intermediate_Hash[2] = 0x98BADCFE;
context->Intermediate_Hash[3] = 0x10325476;
context->Intermediate_Hash[4] = 0xC3D2E1F0;
context->Computed = 0;
context->Corrupted = 0;
return shaSuccess;
}
int SHA1Result(SHA1Context *context, uint8_t Message_Digest[SHA1HashSize]) {
int i;
if (!context || !Message_Digest) {
return shaNull;
}
if (context->Corrupted) {
return context->Corrupted;
}
if (!context->Computed) {
SHA1PadMessage(context);
for (i = 0; i < 64; ++i) {
/* message may be sensitive, clear it out */
context->Message_Block[i] = 0;
}
context->Length_Low = 0; /* and clear length */
context->Length_High = 0;
context->Computed = 1;
}
printf("%x\n", context->Intermediate_Hash[0]);
printf("%x\n", context->Intermediate_Hash[1]);
printf("%x\n", context->Intermediate_Hash[2]);
printf("%x\n", context->Intermediate_Hash[3]);
printf("%x\n", context->Intermediate_Hash[4]);
for (i = 0; i < SHA1HashSize; ++i) {
Message_Digest[i] = context->Intermediate_Hash[i >> 2]
>> 8 * (3 - (i & 0x03));
}
return shaSuccess;
}
int SHA1Input(SHA1Context *context, const uint8_t *message_array, unsigned length) {
if (!length) {
return shaSuccess;
}
if (!context || !message_array) {
return shaNull;
}
if (context->Computed) {
context->Corrupted = shaStateError;
return shaStateError;
}
if (context->Corrupted) {
return context->Corrupted;
}
while (length-- && !context->Corrupted) {
context->Message_Block[context->Message_Block_Index++] =
(*message_array & 0xFF);
context->Length_Low += 8;
if (context->Length_Low == 0) {
context->Length_High++;
if (context->Length_High == 0) {
/* Message is too long */
context->Corrupted = 1;
}
}
if (context->Message_Block_Index == 64) {
SHA1ProcessMessageBlock(context);
}
message_array++;
}
return shaSuccess;
}
void SHA1ProcessMessageBlock(SHA1Context *context) {
const uint32_t K[] = {
0x5A827999,
0x6ED9EBA1,
0x8F1BBCDC,
0xCA62C1D6
};
int t; /* Loop counter */
uint32_t temp; /* Temporary word value */
uint32_t W[80]; /* Word sequence */
uint32_t A, B, C, D, E; /* Word buffers */
/*
* Initialize the first 16 words in the array W
*/
for (t = 0; t < 16; t++) {
W[t] = context->Message_Block[t * 4] << 24;
W[t] |= context->Message_Block[t * 4 + 1] << 16;
W[t] |= context->Message_Block[t * 4 + 2] << 8;
W[t] |= context->Message_Block[t * 4 + 3];
}
for (t = 16; t < 80; t++) {
W[t] = SHA1CircularShift(1, W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16]);
// W[t] = W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16];
}
A = context->Intermediate_Hash[0];//5个初始化常量
B = context->Intermediate_Hash[1];
C = context->Intermediate_Hash[2];
D = context->Intermediate_Hash[3];
E = context->Intermediate_Hash[4];
//分四轮,一共80次分组加密
for (t = 0; t < 20; t++) {
temp = SHA1CircularShift(5, A) +
((B & C) | ((~B) & D)) + E + W[t] + K[0];
E = D;
D = C;
C = SHA1CircularShift(30, B);
B = A;
A = temp;
}
for (t = 20; t < 40; t++) {
temp = SHA1CircularShift(5, A) + (B ^ C ^ D) + E + W[t] + K[1];
E = D;
D = C;
C = SHA1CircularShift(30, B);
B = A;
A = temp;
}
for (t = 40; t < 60; t++) {
temp = SHA1CircularShift(5, A) +
((B & C) | (B & D) | (C & D)) + E + W[t] + K[2];
E = D;
D = C;
C = SHA1CircularShift(30, B);
B = A;
A = temp;
}
for (t = 60; t < 80; t++) {
temp = SHA1CircularShift(5, A) + (B ^ C ^ D) + E + W[t] + K[3];
E = D;
D = C;
C = SHA1CircularShift(30, B);
B = A;
A = temp;
}
context->Intermediate_Hash[0] += A;
context->Intermediate_Hash[1] += B;
context->Intermediate_Hash[2] += C;
context->Intermediate_Hash[3] += D;
context->Intermediate_Hash[4] += E;
context->Message_Block_Index = 0;
}
void SHA1PadMessage(SHA1Context *context) {
if (context->Message_Block_Index > 55) {//如果超过56个字节,那么和MD5一样,也是一直填充完,然后填充到下一轮第56个字节处。
context->Message_Block[context->Message_Block_Index++] = 0x80;
while (context->Message_Block_Index < 64) {
context->Message_Block[context->Message_Block_Index++] = 0;
}
SHA1ProcessMessageBlock(context);
while (context->Message_Block_Index < 56) {//然后补上消息长度的8个字节
context->Message_Block[context->Message_Block_Index++] = 0;
}
} else {
context->Message_Block[context->Message_Block_Index++] = 0x80;
while (context->Message_Block_Index < 56) {
context->Message_Block[context->Message_Block_Index++] = 0;
}
}
context->Message_Block[56] = context->Length_High >> 24;//大端序
context->Message_Block[57] = context->Length_High >> 16;
context->Message_Block[58] = context->Length_High >> 8;
context->Message_Block[59] = context->Length_High;
context->Message_Block[60] = context->Length_Low >> 24;
context->Message_Block[61] = context->Length_Low >> 16;
context->Message_Block[62] = context->Length_Low >> 8;
context->Message_Block[63] = context->Length_Low;
SHA1ProcessMessageBlock(context);
}
#ifdef __cplusplus
}
#endif
int main(){
SHA1Context context;
SHA1Reset(&context);
unsigned char *plainText = (unsigned char *) "Fup1p1";
SHA1Input(&context, plainText, strlen((const char*)plainText));
unsigned char result[16];
SHA1Result(&context, result);
char temp[2] = {0};
char finalResult[41] = {0};
for (int i = 0; i < 20; i++) {
int index = i;
sprintf(temp, "%.2x", result[index]);
strcat(finalResult, temp);
}
printf("%s\n", finalResult);
}
分组密码
分组加密的padding
一般来说,有这么几种填充方式 • Zero Padding (字面意思,后面缺多少个字节就填几个0,但是有个缺陷,就是如果原数据末尾是0,那么就会导致混乱)
• PKCS#7 假设每个区块大小为blockSize 已对齐,填充一个长度为blockSize且每个字节均为blockSize的数据。 未对齐,需要补充的字节个数为n,则填充一个长度为n且每个字节均为n的数据。
• PKCS#5 PKCS#7的子集,就是区块固定位8字节。
分组加密中的模式
当明文的长度大于一个分组长度时,就要考虑加密模式了。 有五种模式:ECB CBC CFB OFB CTR 常用的就前两种。 CFB、OFB、CTR均可将分组密码当流密码使用(所以不需要填充!),虽然他们与流密码的典型构造并不一致。
ECB(Electronic codebook)电子密码本
每个分组之间单独加密,互不关联 2个分组明文一样,结果也一样,那么只需爆破其中1个就可以了 每个分组互不关联,可以分段同时来爆破,不安全 可以通过替换某段密文来达到替换明文的目的
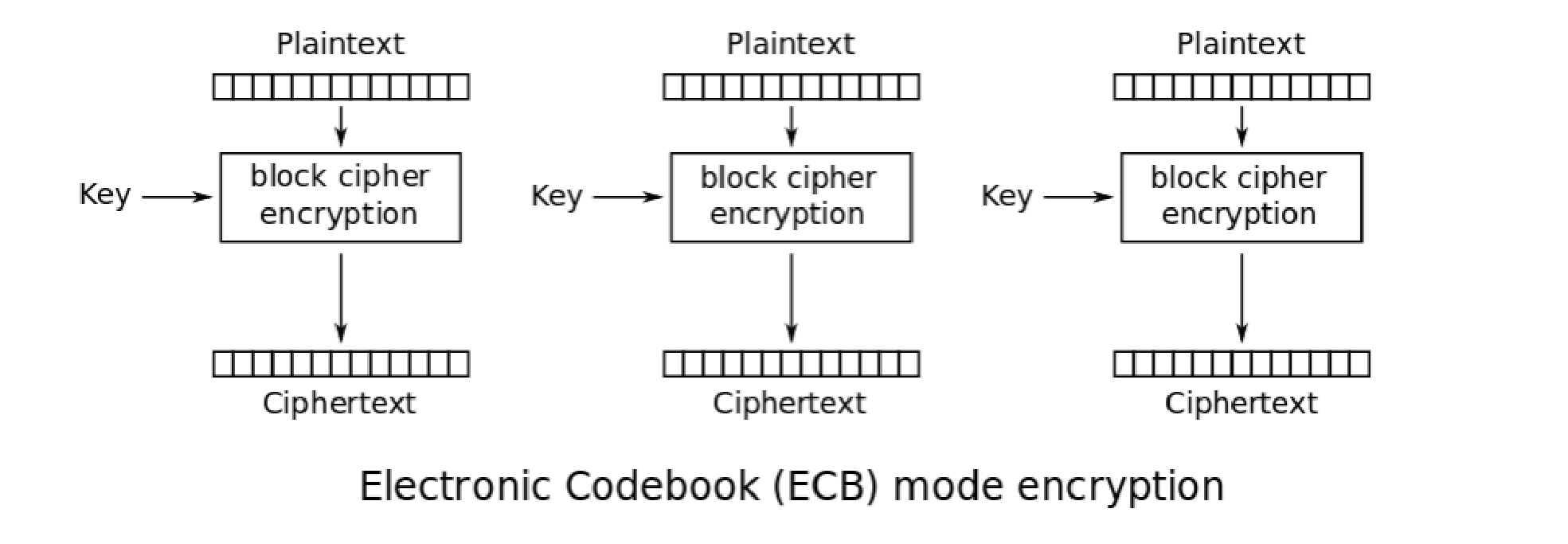
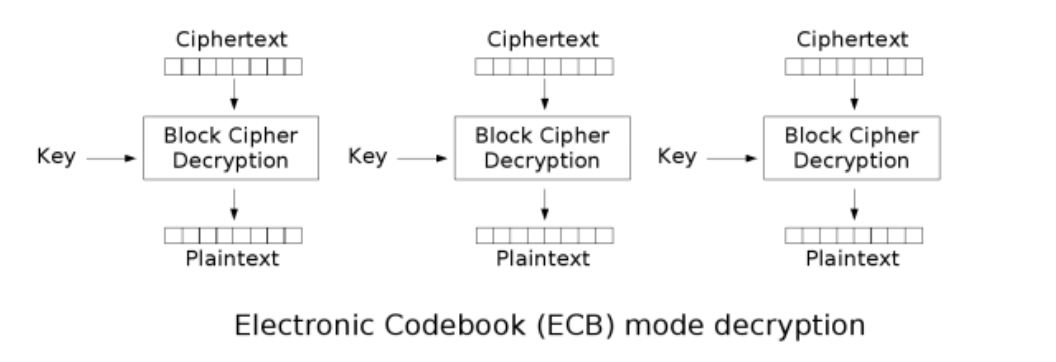
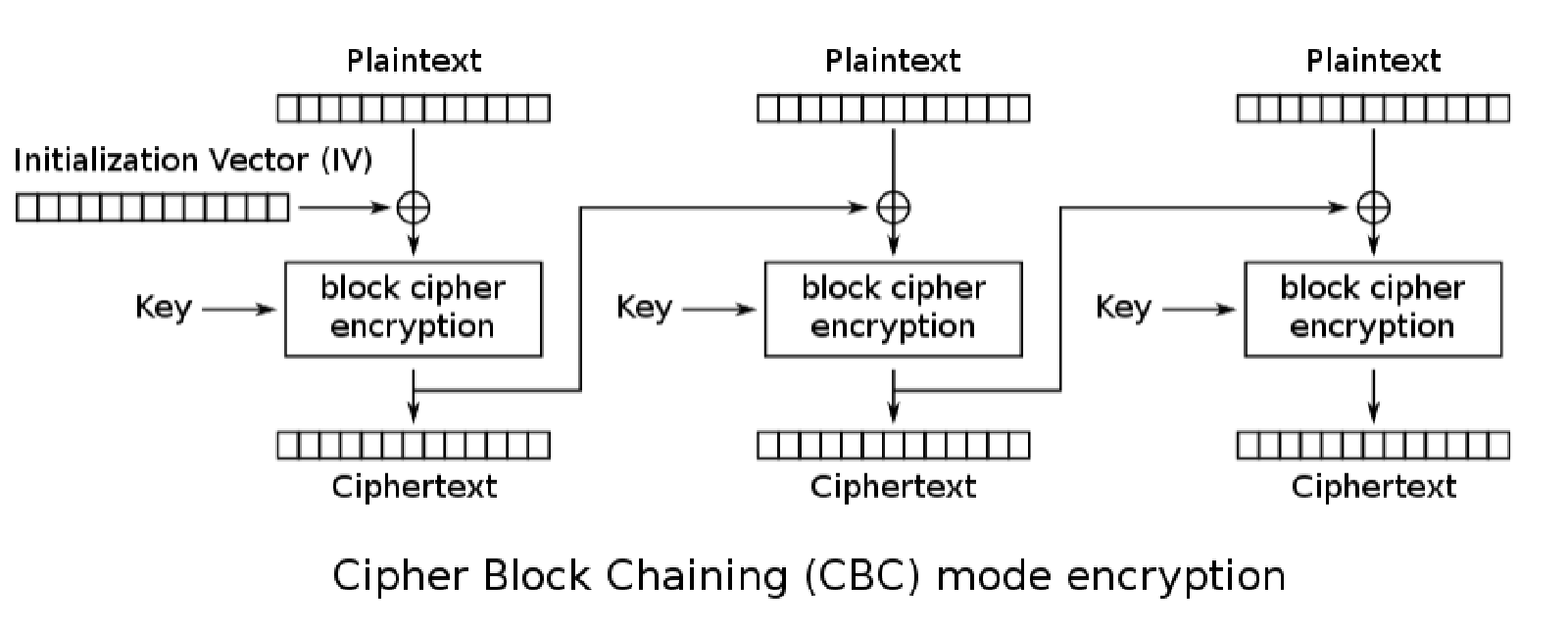
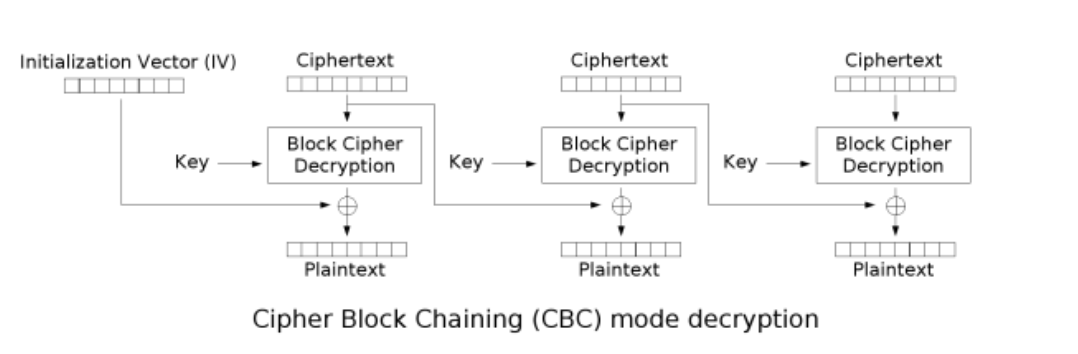
CBC(Cipher Block Chaining)密码块链接
每个明文分组先和上个分组的密文块进行异或,得到的结果进行加密
第1个明文块没有上个分组的密文块,需要指定一个64比特的输入,也就是初始化向量IV
CFB(Cipher Feedback)密文反馈
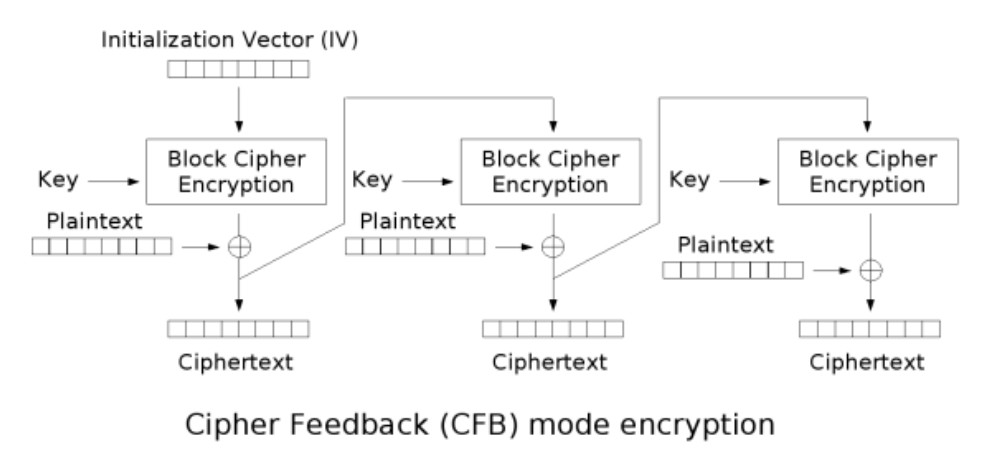
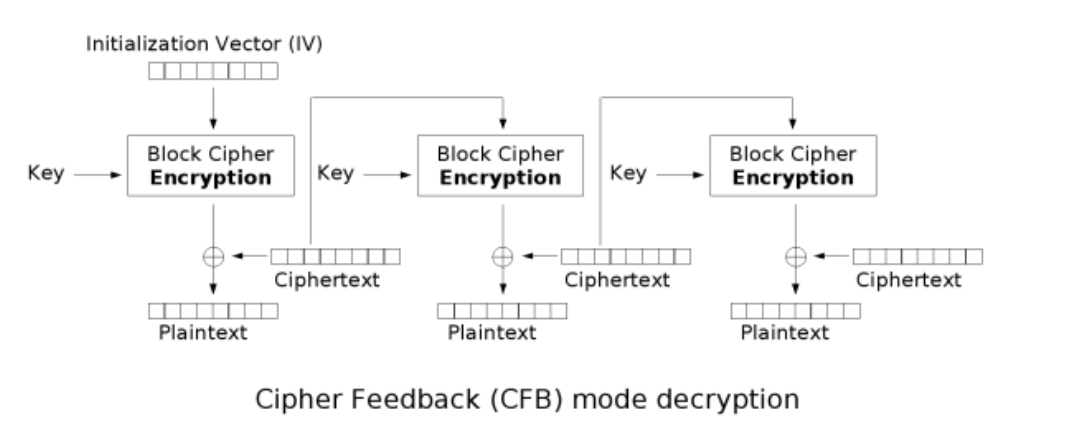 在CFB模式下,首先会对IV进行DES加密得到一个密文块,然后将此密文块与明文的第一个块进行异或运算,得到密文的第一个块。接下来,将得到的密文块再次进行块加密,得到下一个密文块,再与明文的第二个块进行异或运算,得到密文的第二个块。这个过程会一直进行下去,直到整个明文被加密为密文。
而且CFB的解密过程几乎就是颠倒的CBC的加密过程。
在CFB模式下,首先会对IV进行DES加密得到一个密文块,然后将此密文块与明文的第一个块进行异或运算,得到密文的第一个块。接下来,将得到的密文块再次进行块加密,得到下一个密文块,再与明文的第二个块进行异或运算,得到密文的第二个块。这个过程会一直进行下去,直到整个明文被加密为密文。
而且CFB的解密过程几乎就是颠倒的CBC的加密过程。
OFB(Output Feedback)输出反馈模式
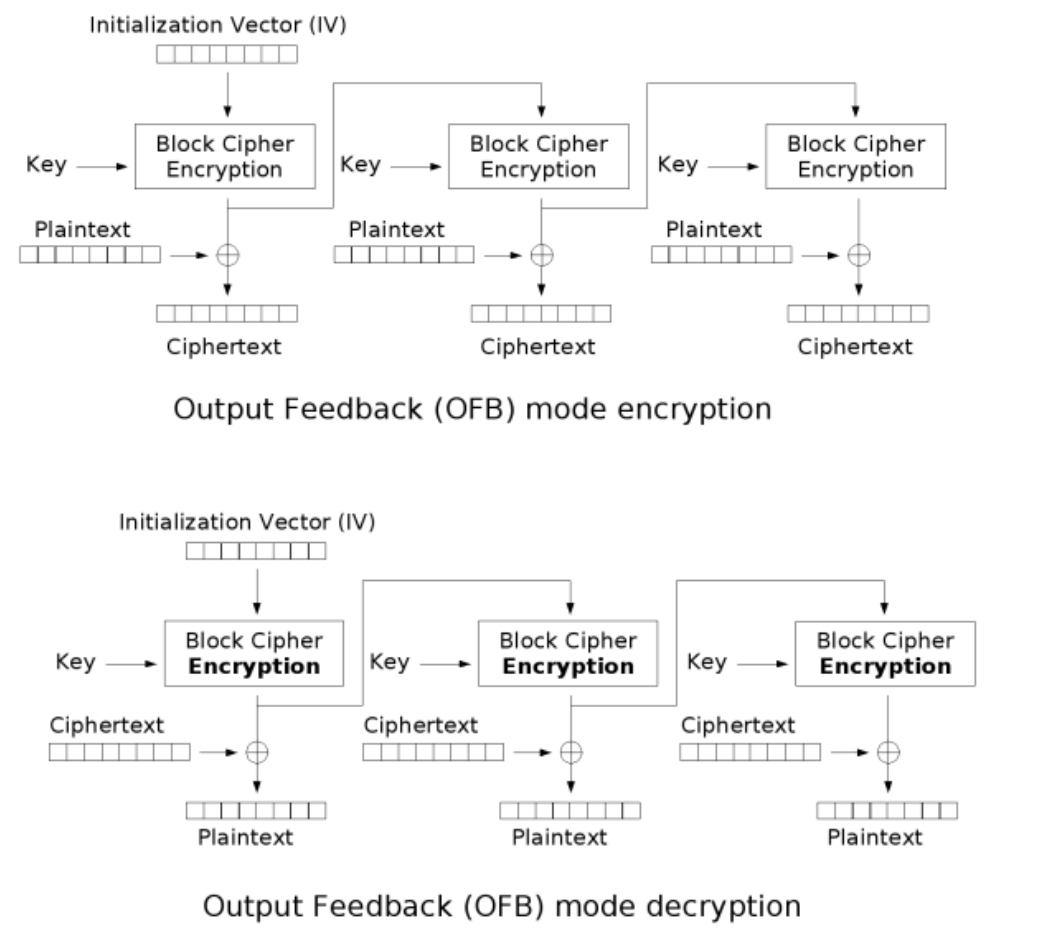 和CFB很像,比起CFB就是多异或了一次。
和CFB很像,比起CFB就是多异或了一次。
DES
前言
一般来说,密钥的长度是64bit,也就是8个字节。然而,其实有效密钥也就只有56bit(为什么,后文会提到!),所以DES因为安全性其实也被淘汰了。
子密钥的生成
首先,将密钥转换成二进制
00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001
密钥初始变换
然后根据PC1表,对密钥进行了一个重新的变换,怎么变换的呢? 就是根据下图这张表来的,
int PC1_Table[56] = {
57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4};
可以这么理解,把二进制的密钥当成一个表,方便理解就把他看出一个64位的s列表好了,那么PC1_Table中所存的每一个值,都相当于一个下标。然后这个表的第8位(8,16,24...)都是一个校验位。所以变换后的密钥,就是s[table[1]] s[table[2]]....去掉校验位,每7位组成一个密钥。 之前的密钥就可以对应出来:
1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111
密钥拆分
1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111
就是将这一段重新编排后的密钥分成两段
C0=1111000 0110011 0010101 0101111 D0=0101010 1011001 1001111 0001111
密钥移位
根据长度为16的key_shift表,又要对上一轮计算的C,D进行循环移位(左移) key_shift = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1];(值也可以是负的哦) C1,D1 根据key_shift[0]可以知道,需要循环左移1位,并且是上一轮的基础上,但是C0,D0其实就是初始值啦。
C1 = 1110000 1100110 0101010 1011111 D1 = 1010101 0110011 0011110 0011110
至于C2D2,也有两种思路: • 对C0D0,分别循环左移2位(1+1) • 对C1D1,分别循环左移1位
然后再将C1D1拼接起来:
1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110
密钥二次变换
然后我们又要根据PC2表,再一次继续变换。
int PC2_Table[48] = {
14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32};
对每一个Cn Dn 都要进行重排,56bit长的Cn Dn就只剩下48bit了(只是压缩而已,并没有校验位,为了和后面的加密算法兼容)...然后给它重命名为Kn。 在后续的DES十六轮运算中,就需要用到Kn
K1 = 000110 110000 001011 101111 111111 000111 000001 110010
K2 = 011110 011010 111011 011001 110110 111100 100111 100101
K3 = 010101 011111 110010 001010 010000 101100 111110 011001
K4 = 011100 101010 110111 010110 110110 110011 010100 011101
K5 = 011111 001110 110000 000111 111010 110101 001110 101000
K6 = 011000 111010 010100 111110 010100 000111 101100 101111
K7 = 111011 001000 010010 110111 111101 100001 100010 111100
K8 = 111101 111000 101000 111010 110000 010011 101111 111011
K9 = 111000 001101 101111 101011 111011 011110 011110 000001
K10 = 101100 011111 001101 000111 101110 100100 011001 001111
K11 = 001000 010101 111111 010011 110111 101101 001110 000110
K12 = 011101 010111 000111 110101 100101 000110 011111 101001
K13 = 100101 111100 010111 010001 111110 101011 101001 000001
K14 = 010111 110100 001110 110111 111100 101110 011100 111010
K15 = 101111 111001 000110 001101 001111 010011 111100 001010
K16 = 110010 110011 110110 001011 000011 100001 011111 110101
DES 中明文的Padding
那么对于DES来说,每组固定是8字节,那么PKCS#7和PKCS#5的效果其实就是一样的咯!
• 如果没有明文,或者明文刚好是8字节的整数倍,这时候都需要再填充一个分组: 即 08 08 08 08 08 08 08 08
• 其他填充的情况 ab cd ef ab cd ef ab 01 ab cd ef ab cd ef 02 02 ab cd ef ab cd 03 03 03 如果明文只有半个字节捏? 比如 ab cd a 那么会给这个半字节前填充一个0 ab cd 0a 05 05 05 05 05
明文的运算
明文的编排
先把明文转成二进制,然后根据表继续置换,哇趣,好熟悉啊。
00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111
根据IP表,对明文进行初始置换
int IP_Table[64] = {
58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7};
又根据表重新排列。
11001100 00000000 11001100 11111111 11110000 10101010 11110000 10101010
然后明文又要分成左右两半,位L0和R0
L0:11001100 00000000 11001100 11111111 R0:11110000 10101010 11110000 10101010
16轮迭代
Ln=Rn-1 Rn=Ln-1 xor f(Rn-1,Kn)
eg
以n = 1为例:
L1 = R0 = 11110000 10101010 11110000 10101010 R1 = L0 xor f(R0, K1)
f函数传入了R0与K1,即第1个子密钥
R0 = 11110000 10101010 11110000 10101010 K1 = 000110 110000 001011 101111 111111 000111 000001 110010
Kn,也就是之前密文变换的结果。
但是R0长度是32bit,K1为48bit,长度不同,那么就没有办法进行按位异或了。
根据E表进行扩展
所以要将32bit的R0扩展成48bit,然后就又需要一个表 E
int E_Table[48] = {
32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1};
E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101
然后进行密钥混合 E(R0) ^ K1
E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101 K1 = 000110 110000 001011 101111 111111 000111 000001 110010 K1 xor E(R0)= 011000 010001 011110 111010 100001 100110 010100 100111
DES算法核心
将上一步的结果分为8块 6bit
B1 = 011000 B2 = 010001 B3 = 011110 B4 = 111010 B5 = 100001 B6 = 100110 B7 = 010100 B8 = 100111
把B1-B8的值当成索引,在S1-S8盒中取值,规则如下:
例子1
以B1为例,值为011000,将它分成0 1100 0,得到 i = 00 即 0 j = 1100 即 12 在S1中查找第0行第12列的值(这里从0开始算)
第0行第12列的值为5 B1 = 5 = 0101
例子2
再以B2为例 B2 = 0 1000 1 i = 01 = 1 j = 1000 = 8
B2 = 12 = 1100 B1在S1中找,B2在S2中找,以此类推
S 表
int S_Box[8][4][16] = {
// S1
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13,
// S2
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9,
// S3
10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12,
// S4
7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14,
// S5
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3,
// S6
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13,
// S7
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12,
// S8
13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
};
get值后
最后8个6比特的值在S盒作用下变成8个4比特的值
S(K1+E(R0)) = 0101 1100 1000 0010 1011 0101 1001 0111
又要按照P表进行重排(怎么这么多重排啊,恼!)
int P_Table[32] = {
16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25
};
P(S(K1 xor E(R0))) = 0010 0011 0100 1010 1010 1001 1011 1011
然后到这里,F函数才算结束了....
F的结果与L0异或
L1 = R0 = 11110000 10101010 11110000 10101010 R1 = Ln-1 xor f(Rn-1,Kn) = 11101111 01001010 01100101 01000100
然后重复16轮,就可以得到一个Ln,Rn的表
L1: 11110000 10101010 11110000 10101010 R1: 11101111 01001010 01100101 01000100 L2: 11101111 01001010 01100101 01000100 R2: 11001100 00000001 01110111 00001001 L3: 11001100 00000001 01110111 00001001 R3: 10100010 01011100 00001011 11110100 L4: 10100010 01011100 00001011 11110100 R4: 01110111 00100010 00000000 01000101 L5: 01110111 00100010 00000000 01000101 R5: 10001010 01001111 10100110 00110111 L6: 10001010 01001111 10100110 00110111 R6: 11101001 01100111 11001101 01101001 L7: 11101001 01100111 11001101 01101001 R7: 00000110 01001010 10111010 00010000 L8: 00000110 01001010 10111010 00010000 R8: 11010101 01101001 01001011 10010000 L9: 11010101 01101001 01001011 10010000 R9: 00100100 01111100 11000110 01111010 L10:00100100 01111100 11000110 01111010 R10:10110111 11010101 11010111 10110010 L11:10110111 11010101 11010111 10110010 R11:11000101 01111000 00111100 01111000 L12:11000101 01111000 00111100 01111000 R12:01110101 10111101 00011000 01011000 L13:01110101 10111101 00011000 01011000 R13:00011000 11000011 00010101 01011010 L14:00011000 11000011 00010101 01011010 R14:11000010 10001100 10010110 00001101 L15:11000010 10001100 10010110 00001101 R15:01000011 01000010 00110010 00110100 L16:01000011 01000010 00110010 00110100 R16:00001010 01001100 11011001 10010101
然后将L16和R16换一下顺序,结果为R16L16
R16L16 = 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100
然后最后根据FP表进行行末的置换
10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101
int FP_Table[64] = {
40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25};
上述数据的十六进制形式为
85 e8 13 54 0f 0a b4 05
3DES (Triple DES)
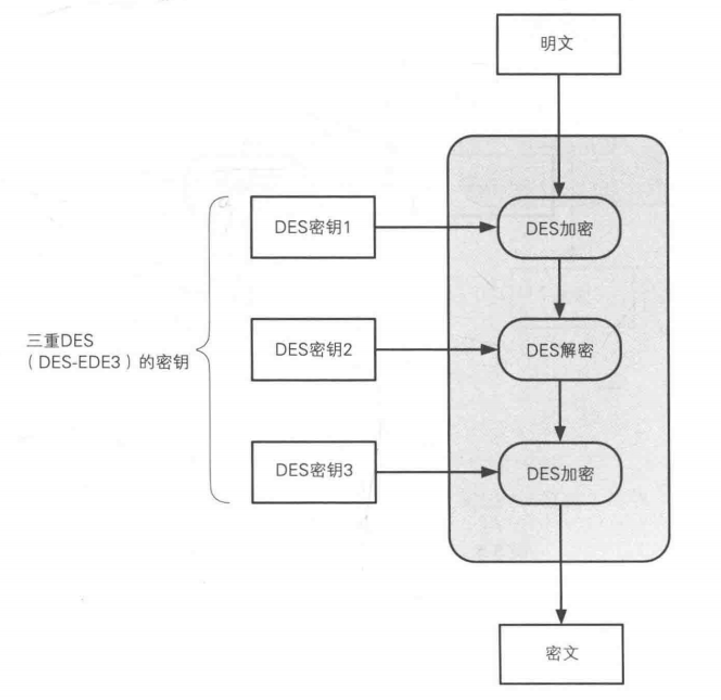 1.密钥24个字节,相当于3个DES的密钥
1.密钥24个字节,相当于3个DES的密钥
2.3DES的处理流程,每次使用一个DES的密钥 DES加密-->DES解密-->DES加密 (如果第一个密钥和第二个密钥一样,就相当于啥都没干了QAQ)
AES
即Advanced Encryption Standard,高级加密标准
-
AES算法的一些特点 1.1 在一个分组长度内,明文的长度变化,AES的加密结果长度都一样 1.2 密钥长度128、192、256三种,如果少1个十六进制数,会在前面补0 1.3 分组长度只有128一种 1.4 密文长度与填充后的明文长度有关,一般是16字节的倍数
-
Rijndael算法也叫AES算法 Rijndael算法本身分组长度可变,但是定为AES算法后,分组长度只有128一种
-
DES中是针对bit进行操作,AES中是针对字节进行操作
-
AES128 -> 10轮运算、AES192 -> 12轮运算、AES256 -> 14轮运算
加密流程
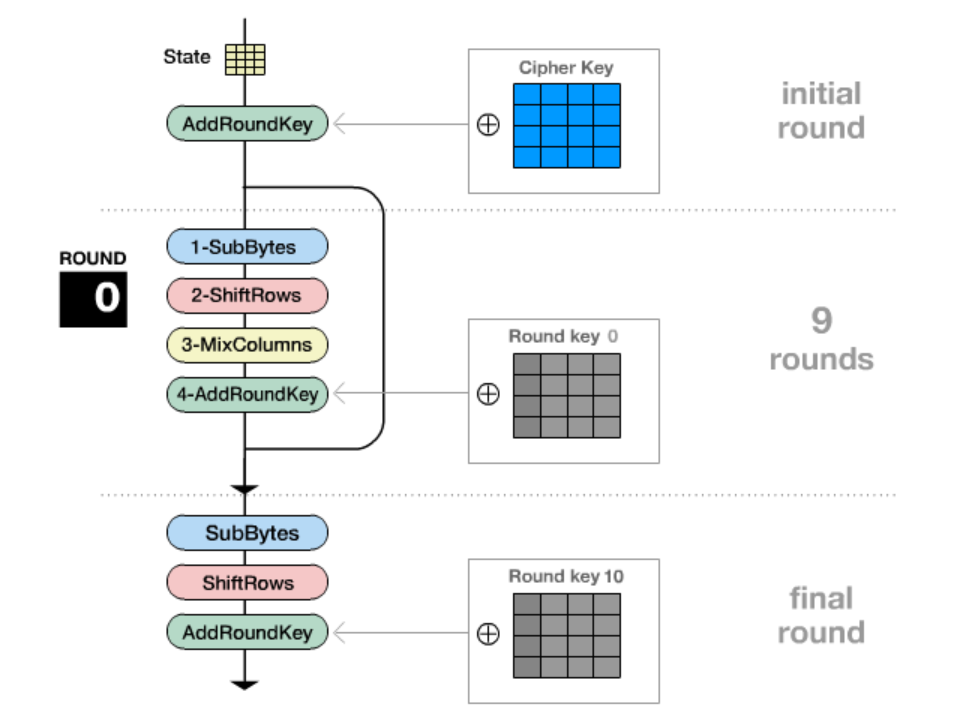
一.初始变换
1.明文state化
明文和密钥变成4*4的矩阵,而且是按顺序竖着放进矩阵里去。
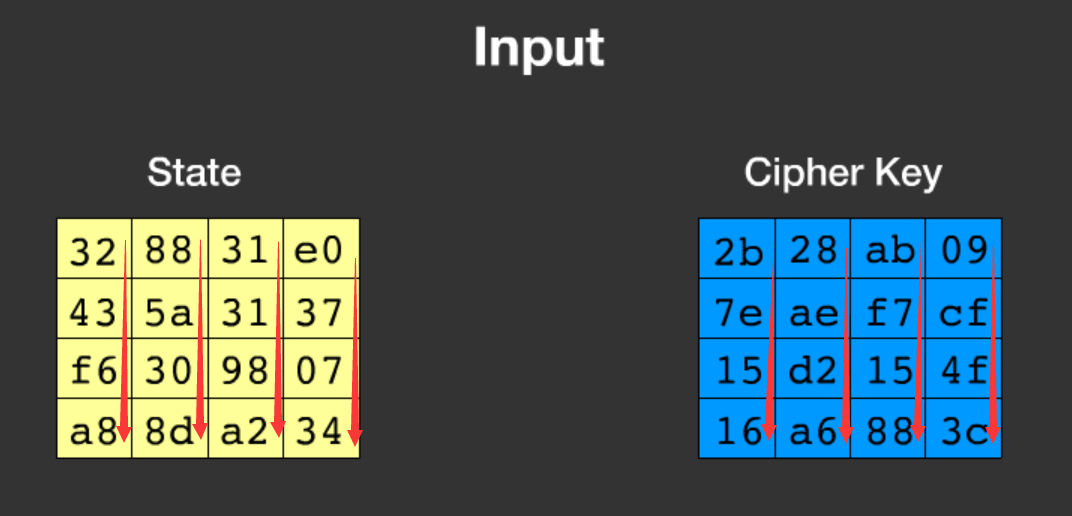
2.初始轮密钥加
与种子密钥K异或(如果是CBC模式先与iv异或)
二.前9/11/13轮运算
1.SubBytes(替换S盒)
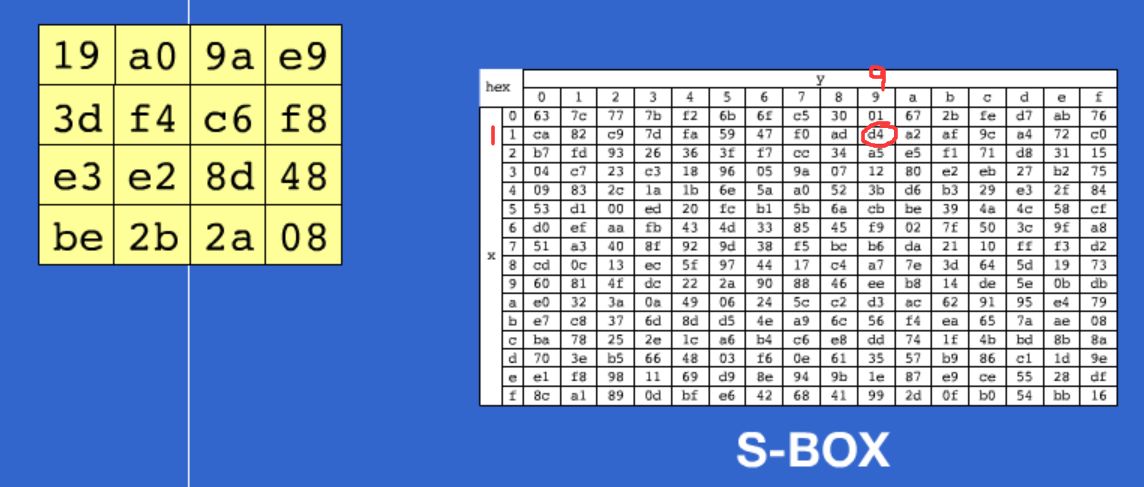
2.ShiftRows(行移位)
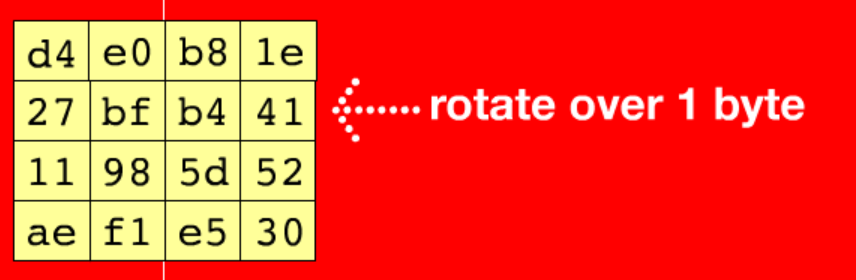
第一行不变 第二行循环左移1位 第三行循环左移2位 第四行循环左移3位
3.MixColumns(列混合)
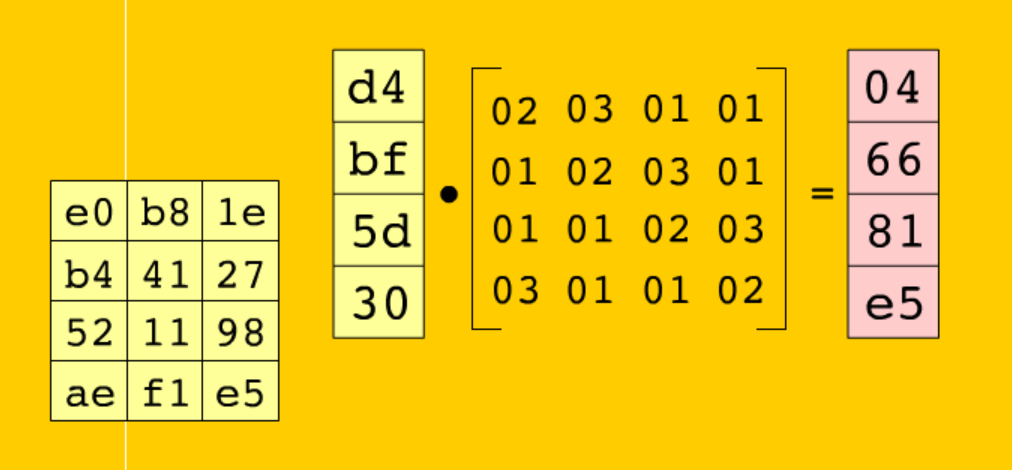 特征:会存在一个4*4的数组,然后会做一个伽罗华域乘法运算(其中会用到两个常量 0x1b 和0x80,这两个值算是一个特征了)
特征:会存在一个4*4的数组,然后会做一个伽罗华域乘法运算(其中会用到两个常量 0x1b 和0x80,这两个值算是一个特征了)
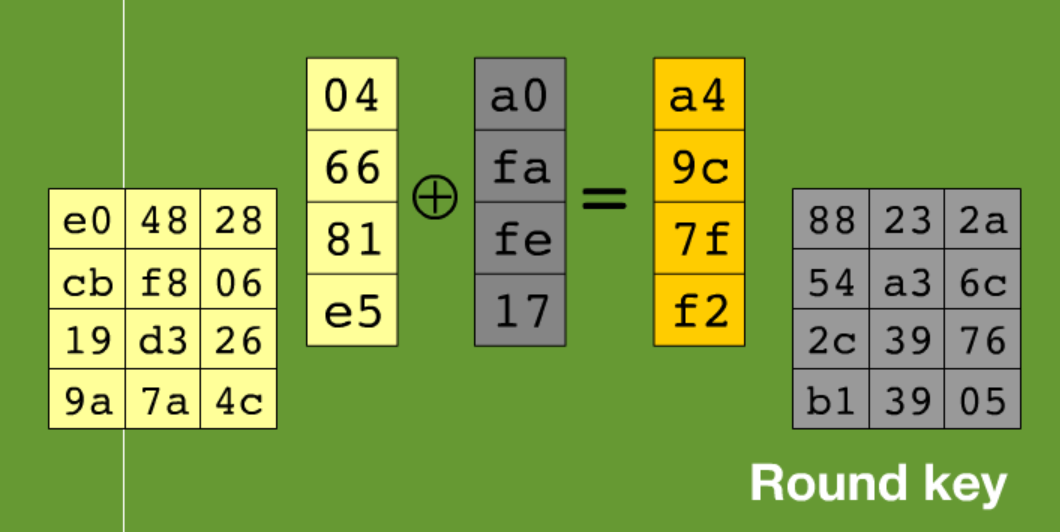
4.AddRoundKey(轮密钥加) 即与子密钥K1~Kn-1进行异或
这个比较好懂,只是简单的异或。



评论区